반응형
Probability
- 사건집합(Event Set) : 모든 가능한 사건의 집합
- Ω={e1,e2,⋯,eD}
- 이벤트 갯수가 유한일때 : 이산(Descrete)
- 이벤트 갯수가 무한일때 : 연속(Continuous)
- 확률변수(Random Variable): 사건집합 안에 속하지만 정의되지 않은 어떤 값
- 확률(Probability): 사건집합에 속한 확률변수에게 어떤 값을 지정해주는 함수입니다.
- p(X=ei)
- 특성(Properties)
- Non-negatives: p(X=ei)≥0 , 확률은 비음수입니다.
- Unit volume: ∑e∈Ωp(X=e)=1 , 모든 확률의 합은 1이 되어야 합니다.
- 결합확률(Joint probability): p(Y=ejY,X=eiX)
- 조건부 확률(Conditional probability): p(Y=ejY∣X=eiX)
- 한계 확률(Marginal probability): p(Y=ejY)=∑e∈ΩXp(Y=ejY,X=eiX)
Loss Function
- 지도학습은 Input(x) 값을 넣었을 때 Output(y) 값을 산출 하는 것입니다. 하지만 조금만 다르게 생각해서, Input(x) 값이 주어졌을 때 의 Output(y) 값이 y’ 일 확률을 구하는 것으로 생각할 수 있습니다.
- fθ(x)= ? → p(y=y′∣x)= ?
- 어떤 확률 분포들이 있을까요?
- 이진 분류: 베르누이(Bernoulli) 분포
- 다중 분류: 카테고리(Categorical) 분포
- 선형 회귀: 가우시안(Gaussian) 분포
- 다항 회귀: 가우시안 믹스쳐(Mixture of Gaussians)
- 인공신경망 모델이 조건부 확률 분포를 출력하면 이를 사용해서 비용함수를 정의 할 수 있습니다.
- 최대한 모델이 출력한 조건부 확률 분포가 훈련 샘플의 확률분포와 같게 만드는 것입니다. 즉 모든 훈련 샘플이 나올 확률을 최대화 하는 것입니다.
- 이렇게 함으로서 자동으로 비용함수를 정의 할 수 있습니다. 이를 최대 우도 추정(Maximum Likelihood Estimation)라고 합니다.

- Log 를 사용하는 이유는 여러가지가 있지만, 이 강의에서는 이야기 하지 않겠습니다.
- 또한 최소화를 하기 위해서 앞에 마이너스 부호를 붙여줍니다. (-1 을 곱합니다.)
- 최종적으로, 비용함수는 음의 로그확률(Negative Log-probabilities)의 합으로 결정됩니다.
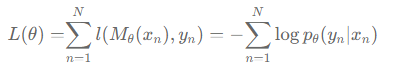
반응형
'Data Science > NLP' 카테고리의 다른 글
| Gradient-Based Optimization (0) | 2022.03.28 |
|---|---|
| Backpropagation (0) | 2022.03.28 |
| Optimization methods (0) | 2022.03.28 |
| Hypothesis Set (0) | 2022.03.28 |
| Basic ML/DL Overview (0) | 2022.03.28 |

댓글